目次
はじめに
今回も、応用情報技術者試験の過去問を解いていきます。
今回は「木構造の再帰処理」に関する問題にチャレンジしました。
問題(R6年度 応用情報技術者試験 春期 午前 問6)
問6
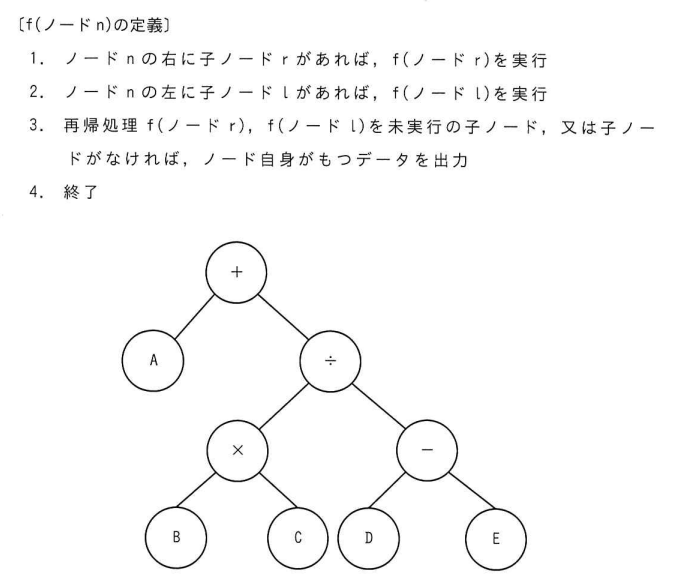
各ノードがもつデータを出力する再帰処理 f(ノード n) を定義した。
この処理を、図の2分木の根(最上位のノード)から始めたときの出力はどれか。
選択肢
ア:+ ÷ - E D × C B A
イ:A B C × D E - ÷ +
ウ:E - D ÷ C × B + A
エ:E D - C B × ÷ A +
解答
正解:エ
解説
🔍 再帰処理の基本的な考え方
「再帰処理(さいきしょり)」とは、関数(処理)自体が“自分自身”を呼び出すこと。
今回のような木構造をたどるときにとても使いやすい方法です。
でも再帰処理では「呼び出したあとすぐ戻るのではなく“保留”になる」という重要な特徴があります。
→ この「保留(スタックに積まれる)」の仕組みが分かると、今回の問題の動きも理解しやすくなります!
📚 スタックとは?
スタックとは:
- 一番最後に積んだものが、最初に取り出される(LIFO:Last In, First Out)構造
- 再帰呼び出しでは「まだ終わっていない呼び出し」がどんどん積まれていく
- 下から順に戻っていく
🌳 今回の問題の流れ
【再帰呼び出しと戻り図】
呼び出し開始 → f(+) ← スタックに積む
└── 呼び出し f(÷) ← スタックに積む
└── 呼び出し f(-) ← スタックに積む
└── 呼び出し f(E) ← スタックに積む → 出力 [E] → 戻る
└── 呼び出し f(D) ← スタックに積む → 出力 [D] → 戻る
→ 出力 [-] → 戻る
└── 呼び出し f(×) ← スタックに積む
└── 呼び出し f(C) ← スタックに積む → 出力 [C] → 戻る
└── 呼び出し f(B) ← スタックに積む → 出力 [B] → 戻る
→ 出力 [×] → 戻る
→ 出力 [÷] → 戻る
└── 呼び出し f(A) ← スタックに積む → 出力 [A] → 戻る
→ 出力 [+]
一部の処理まで順を追って解説
【f(ノード n) の定義 再掲】
1️⃣ 右に子ノード r があれば、f(ノード r) を実行
2️⃣ 左に子ノード l があれば、f(ノード l) を実行
3️⃣ 未実行の子ノードがなければ、自分のデータを出力
4️⃣ 終了
【対象の木構造 全体図(再掲)】

🌟 スタート地点 → f(+) 呼び出し!
🔸 ステップ 1: f(+) の呼び出し開始
いまノード:+
✅ 1️⃣ 右に子ノード ÷ がある → f(÷) を実行!
→ f(+) はスタックに積まれたまま、 f(÷) 呼び出しへ
🔸 ステップ 2: f(÷) の呼び出し開始
いまノード:÷
✅ 1️⃣ 右に子ノード - がある → f(-) を実行!
→ f(÷) はスタックに積まれたまま、 f(-) 呼び出しへ
🔸 ステップ 3: f(-) の呼び出し開始
いまノード:-
✅ 1️⃣ 右に子ノード E がある → f(E) を実行!
→ f(-) はスタックに積まれたまま、 f(E) 呼び出しへ
🔸 ステップ 4: f(E) の処理
いまノード:E(葉ノード)
✅ 1️⃣ 右なし → スキップ
✅ 2️⃣ 左なし → スキップ
✅ 3️⃣ 未実行の子がない → E を出力!
→ 出力:[E]
→ f(E) 完了 → 呼び出し元(f(-))へ戻る
🔸 ステップ 5: f(-) に戻る
戻ってきた f(-) の状態:
✅ 右の子(E)は 実行済み
✅ 2️⃣ 左に子ノード D がある → f(D) を実行!
🔸 ステップ 6: f(D) の処理
いまノード:D(葉ノード)
✅ 1️⃣ 右なし → スキップ
✅ 2️⃣ 左なし → スキップ
✅ 3️⃣ 未実行の子がない → D を出力!
→ 出力:[D]
→ f(D) 完了 → 呼び出し元(f(-))へ戻る
🔸 ステップ 7: f(-) に戻る(左右とも完了)
戻ってきた f(-) の状態:
✅ 右の子 E → 実行済み
✅ 左の子 D → 実行済み
✅ 3️⃣ 未実行の子がない → - を出力!
→ 出力:[-]
✅ ここまでの出力結果
E → D → -
✅ これを繰り返すと…
E → D → - → C → B → × → ÷ → A → +
正解:エ
となります。
💡 迷いやすいポイント
✅ よくある疑問 → 「E にたどり着いたあと、次は D を処理?それとも - を出力?」
→ これは「親ノード(-)の中で、“未実行の子” があるかどうか」を見るのがコツ!
✅ E から戻ってきたとき、f(-) の処理はまだ「左の子 D」を未実行なので、
→ 次は D を呼び出すべき!
→ 左右両方の子を実行し終えた時点で、はじめて「-」が出力される。
問題の用語解説
| 用語 | 意味 |
|---|---|
| 木構造(ツリー構造) | ノードが親子関係を持つデータ構造。 |
| 根(root) | 最上位のノード(+) |
| 葉(leaf) | 子を持たないノード(A, B, C, D, E) |
| 再帰処理 | 自分自身を呼び出す処理。木構造や分割統治法で使う。 |
| スタック | LIFO のデータ構造。再帰呼び出しの時に「保留」に使われる。 |
| 未実行の子 | まだ呼んでいない子ノードのこと。親ノード出力はその後になる。 |
体系的位置づけ

まとめ
✅ 再帰処理は「自分自身を呼ぶ」処理方法
✅ 呼び出した時に「保留(スタックに積む)」の動きを理解するのがカギ
✅ 未実行の子が残っているうちは親は出力しないというルールを押さえる
✅ 木構造の問題は毎年〜隔年で出やすいテーマなので、再帰+スタックの流れを身につけておくと安心!
参考情報
- IPA 応用情報技術者試験 過去問題:
https://www.ipa.go.jp/shiken/mondai-kaiotu/2024r06.html



コメント