目次
はじめに
今回も「応用情報技術者試験」の過去問にチャレンジしていきます。
今回は アルゴリズムの流れ図(フローチャート) の問題です。
ループ処理やフローチャート記号の正しい読み取りが重要になる問題なので、しっかり確認していきます。
問題
問5
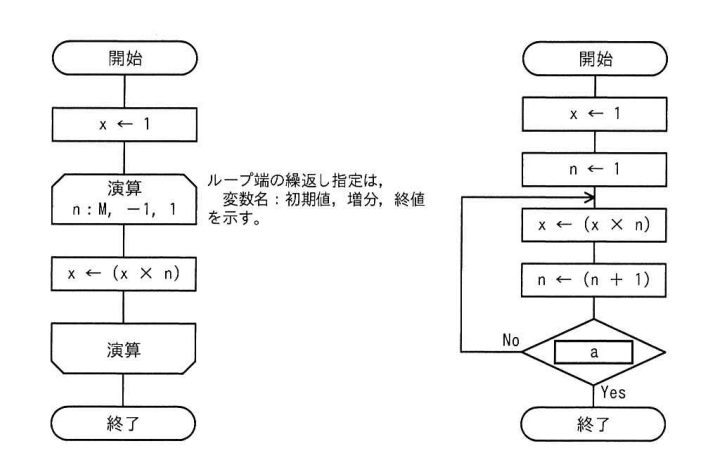
正の整数 M に対して、次の2つの流れ図に示すアルゴリズムを実行したとき、結果 x の値が等しくなるようにしたい。
a に入れる条件として適切なものはどれか。
【選択肢】
- ア)n < M
- イ)n > M − 1
- ウ)n > M
- エ)n > M + 1
解答
ウ)n > M
が正解です。
解説
左右のフローチャートは M!(Mの階乗) を計算しています。
左の流れ図の意味
左の流れ図は for文型のループ処理 になっています。
図中の n : M, -1, 1 という記述は次の意味です:
| 項目 | 内容 |
|---|---|
| 変数名 | n |
| 初期値 | M |
| 増減量 | -1(1ずつ減らす) |
| 終了条件 | 1まで繰り返す |
つまり次の処理をしているのと同じ:
for ( n = M ; n ≥ 1 ; n-- ) { x = x × n }
右の流れ図の意味
右の流れ図は while文型のループ処理 になっています。
ループ内で:
x ← x × n n ← n + 1
を繰り返して、条件判定(a) によってループを抜ける形です。
重要ポイント:
- 判定は n ← n + 1 の後 に行われます。
各選択肢の動作(M=3の場合の例)
| 選択肢 | 実行結果 | 理由 |
|---|---|---|
| ア) n <3 | すぐ終了してしまう | 初期n=1でも条件を満たし、1回も掛け算せずに終了する |
| イ) n >2 | 判定はn+1の後なので、M=3に到達する前に判定で終了 | 最後の掛け算(n=3)が実行されず、1個手前までしか計算できない |
| ウ) n >3 | n=3まで掛け算を行い、その後に判定で終了 | ちょうど M! が計算される → 正解 |
| エ) n >4 | n=4 まで掛け算をしてしまい M+1 の項まで掛けてしまう | 掛けすぎになるため誤り |
問題の用語解説
フローチャートに出てくる図形の意味
| 図形の形状 | 名前・意味 |
|---|---|
| 左上・右上の角が丸い長方形 | 端子(開始) → 開始位置を示す |
| 左下・右下の角が丸い長方形 | 端子(終了) → 終了位置を示す |
| ふつうの長方形 | 処理(プロセス) → 代入や計算などの操作 |
| ひし形 | 判断(条件分岐) → Yes/No の判定 |
| 左右の角が斜めカットされた横長長方形 | ループ(for文風の省略形) → カウント付き繰返し処理を表す(例:n : M , -1 , 1) |
体系的位置づけ
この問題は:
- アルゴリズム分野
- フローチャート記法の理解
- ループ処理(繰返し処理)の理解
に分類される内容です。
応用情報技術者試験でも 頻出テーマ なので、
フローチャート記号の読み取り+ループの処理順を理解しておくことが重要です!
まとめ
- 左の流れ図は for文型ループ(カウント付きループ)
- 右の流れ図は while型ループ(条件判定ループ)
- 判定位置(n+1の後に判定)が重要なポイント
- 正解は「ウ)n > M」で、 M!(Mの階乗) を正しく求められる!
- フローチャートの各図形の意味も確認しておこう!
参考情報
- IPA 応用情報技術者試験 過去問題:
https://www.ipa.go.jp/shiken/mondai-kaiotu/2024r06.html



コメント